Early Maths – Getting started with… Number bonds to 5

What are number bonds to 5?

The term ‘number bonds’ refers to pairs of numbers that make up a total. Thus, ‘number bonds to 5’ means all the pairs of numbers that make the totals 1, 2, 3, 4, and 5. Here they are:

Number bonds of 1:                  1 and 0

Number bonds of 2:                  1 and 1              2 and 0

Number bonds of 3:                  1 and 2              3 and 0

Number bonds of 4:                  1 and 3              2 and 2             4 and 0

Number bonds of 5:                  1 and 4              2 and 3             5 and 0

All these pairs have their inverses, eg: 0 and 1, as well as 1 and 0.

There are four key areas of early number, which in reality interrelate:

• Counting
• Cardinality
• Composition
• Comparison

The National Centre of Excellence in Teaching Mathematics (NCETM) outline these key areas in this article.

Number bonds form part of the composition of numbers, although they also have connections to counting, subitising (read more in my blog about subtising) and comparison. The composition of number is the understanding that one number can be made up from – composed from – two or more smaller numbers. Number bonds (pairs of numbers) are part of this broader area, as the composition of 5, for example, includes learning about 5 as being made up of 1, 1, 1 and 2, as well as the pairs of smaller numbers.

This is important, as it illustrates perfectly how crucial objects and context are in supporting children to learn their number bonds to 5. At the heart of the ‘what to do’ section below, are context and using a range of manipulatives.

Why are number bonds important?

The word ‘fluency’ is more often associated with speaking, writing and reading with ease, but fluency is also, along with reasoning and problem solving, one of the three aims of the statutory mathematics National Curriculum for 5 – 16 year olds (DoE 2013).

Mathematical fluency refers to efficiency, accuracy and confidence in tackling mathematical problems. This includes us being able to easily access our knowledge of facts such as number bonds. Knowledge of number bonds is key in establishing later numerical fluency. If you know 3 and 2 together make a total of 5, it is later possible to know – to reason – that 20 and 30 make a total of 50, without counting out 50 items.

Number bonds are also important in building young children’s enjoyment and confidence in mathematics more generally. Encouraging children to quickly recognise arrangements of small amounts up to five (to subitise – see my blog about this) is the basis on which to build a young child’s number bond understanding, and sets up the process of becoming confident and fluent with number bonds.

What to do? 

These ideas are based on building young children’s confidence and enjoyment alongside their competence. I find repetition of a simple game, which is enjoyed by both children and adults, and that can later be played independently, to be a powerful way of fostering fluency with children. Find one game you all enjoy and gradually vary this over time, making alterations based on your observations of the children when they play. Once you begin to work with 4 and more as your number bond total, it is best to stick to one quantity in one sitting, ie, work with 4 items for a few days or longer, until children are confident with the bonds to 4, and not counting each sub-group, before moving on to play with 5 items. The aim is that they are able to quickly and confidently say each pair.

Activity ideas:

Hiding games

• Play a version of Hughes’ box game described above, starting with 3 identical bricks and moving 1, 2, 3 bricks in and out of the box, asking the child “Now (I have taken 1 out / added 1 in) how many bricks are in the box?” Don’t forget to include removing or adding no (zero) bricks, as children find zero fascinating and amusing.
• Vary the materials you play with, making sure the items you play with are identical each time, encouraging children to play independently by providing each child with a bowl and 3 identical items and asking them to ‘say what they can see’.
• The context can be adapted effectively to moving play-people (or real children!) in and out of a tent.

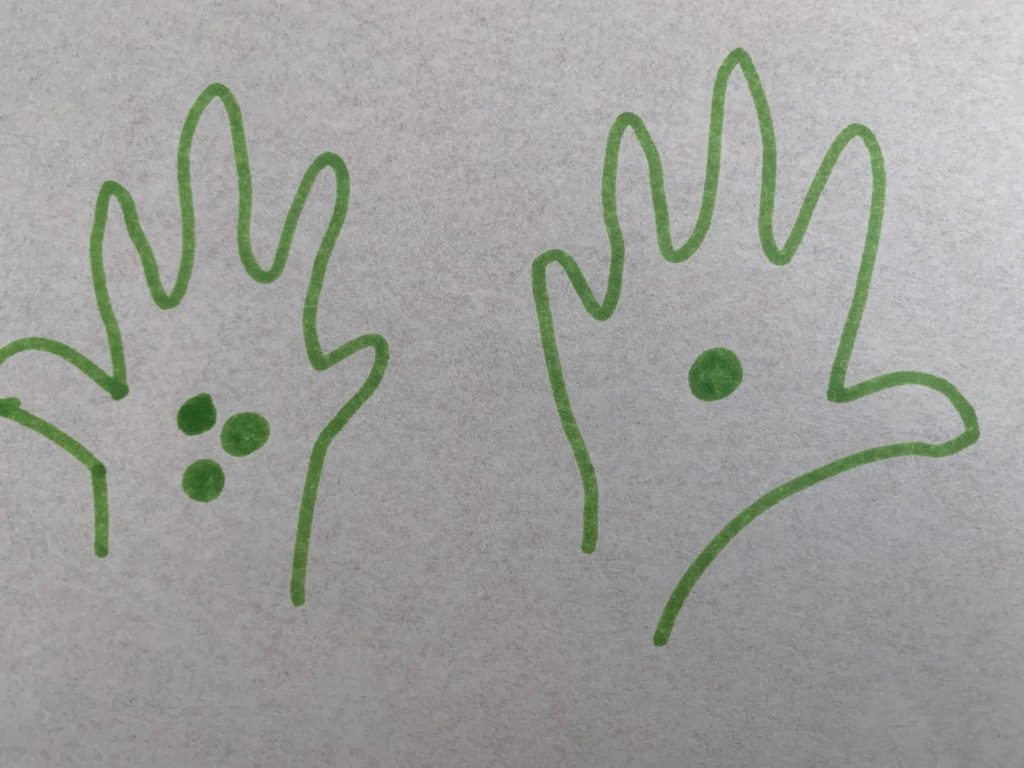
A hand game

• With a given quantity of similar counters or pebbles, children take it in turns to decide how to separate these in different ways, open their hands one at a time, saying how many pebbles they see in each hand, eg: “Three … and one – four!”. Emphasise the overall quantity each time.
• This can be adapted to giving each child a stick of, for eg, 4 interlocking cubes in one colour only. Children break their stick into two and say what they have done.

Egg Box Maths

• Strictly speaking this is experience of number bonds of 6. You could cut the boxes down to work with bonds of 4.
• Provide egg boxes, and cubes or counters in two colours only. Children fill the egg boxes with various combinations of two colours of counter and describe what they see. Encourage them to see the two small totals in the box and to say how many altogether, eg: “I see 3 orange and 3 blue, 6 altogether”.

Number Sticks

• Provide cubes or blocks in two colours only. Make lots and lots of sticks of 3 (or 4, or 5).
• What different sticks can we make? How are they different? How are they the same? Talk about the pairs of numbers in each stick and the overall quantity each time.

Beans up

• Each child has a cup and 3 (later, 4 then 5) butter beans coloured on one side only. They shake their cup of beans, tip it out and say how many land ‘gold up’ and how many ‘gold down’. Emphasise the overall quantity each time.

Time for Snack

• Snack time is an ideal context for children to explore and apply their developing knowledge of number bonds.
• Give out the snacks to emphasise the pairs of numbers they have been learning, for eg: “Here are 2 apple slices for you and another 2, that’s 4 altogether.” “If I now give you 1 more cherry, can you tell me how many will you have then?”

The ‘Boss and x-ray eyes’ game

• This game links the number bonds the children have been learning to numerals, it comes after the children have had a lot of experiences of the other activities.
• Provide up to 5 items, a box lid and numerals 0,1,2,3,4, and 5 written on cards.
• One child starts as the Boss. The partner (with x-ray eyes!) goes away until they are called back. The Boss counts the correct amount of items into the tray and separates these into two groups. They choose the correct number cards for both groups and place one card in the box. Hide the other card. Call back your partner. With their X-ray eyes, they should look in the box and work out which number is written on the hidden card. Finish by drawing attention to the total by saying something like: “4 and 1, 5 altogether.” Swap roles.

All these experiences will make a real difference to your children’s numerical understanding alongside their fluency and confidence with numbers. Enjoy all your mathematical moments together.